Σε έναν τόπο πολύ μικρό ανάμεσα στις ακτές της Ασίας και κάποια μεσογειακά νησιά μία ανακάλυψη έπεσε σαν κεραυνός πριν από δύο χιλιετίες. Κι αυτή η ανκάλυψη συνδέεται με μία μοναδική λέξη.

Όταν μιλάμε σήμερα για επιστήμη… λέμε π.χ. “Βιολογία” – η επιστήμη της ζωής. Λέμε “Κοσμολογία” – η επιστήμη του κόσμου. Λέμε “Τοπολογία” – η επιστήμη των τόπων. Σε κάθε περίπτωση, όμως, λέμε “-λογία”.

Σημαίνει τη σαφή ομιλία, που οι Έλληνες την έλεγαν “λόγο”. Προσθέτουμε το “-λογία“ για να υποδηλώσουμε μια επιστήμη. “Λόγος” σε απλά ελληνικά θα πει λεκτική έκφραση ή ομιλία… μα στη γλώσσα της επιστήμης σήμαινε τη σχέση α προς β. Ή, ακόμα καλύτερα, τη διπλή σχέση α/β=γ/δ. Αυτό το ονόμαζαν αναλογία. Και ο λόγος, αυτή η σχέση, επινοήθηκε σε αυτόν ακριβώς τον τόπο, και ιδού πως:

Ας πάμε στη νήσο Σάμο, πολύ κοντά στα σημερινά τουρκικά παράλια. Στη Σάμο γεννήθηκε ο Πυθαγόρας, που επινοεί την Αριθμητική και στα πλαίσιά της επινοεί τη σχέση 2/4=α/β. Επινοεί ακριβώς τη σχέση 2/4=8/16. Επινοεί τη σχέση ανάμεσα σε ακέραιους αριθμούς και αριθμούς που κάποτε θα ονομαστούν κλάσματα ή λόγοι. Και όλη η θεωρία των αριθμών θα εκπορευτεί από αυτό.

Στην απέναντι ελληνική πλευρά που σήμερα κατέχει η Τουρκία, θα γεννηθεί ένας άλλος άντρας, ο Θαλής. Γεννημένος στην Μίλητο επινοεί το περίφημο θεώρημα του Θαλή περί όμοιων τριγώνων. Και πάλι ο “λόγος”… γιατί αυτή προς εκείνη την πλευρά ισούται με αυτήν προς εκείνη, οπότε έχουμε τον ίδιο “λόγο”.

Κοντά στην Μίλητο βρίσκεται μια άλλη ελληνική πόλη, η Έφεσος. Εκεί γεννιέται ο Ηράκλειτος. Ο Ηράκλειτος είναι φυσικός, ο πρώτος πολύ σπουδαίος φυσικός στην ιστορία. Περιγράφει τα φυσικά φαινόμενα, την εξέλιξη των πραγμάτων, το πέρασμα του χρόνου, ό,τι είναι ορατό. Και πίσω από κάθε φαινόμενο αναζητά την αιτία. Αυτή την αιτία την ονομάζει λόγο. Αριθμητικό λόγο, γεωμετρικό λόγο, φυσικό λόγο. Αν κατεβούμε κι άλλο στα παράλια, φτάνουμε σε ένα κατεστραμμένο σήμερα λιμάνι, την Κνίδο, όπου ο Εύδοξος ο Κνίδιος επινοεί ξανά τον λόγο. Κι αυτός ο κάπως πιο περίπλοκος λόγος θα γεννήσει την σύγχρονη Αλγεβρική θεωρία και είναι ο αλγεβρικός λόγος.

Ας ανεβούμε τώρα την ακτή κι ας γυρίσουμε στα νησιά. Δίπλα στη Σάμο βρίσκεται ένα νησί που λέγεται Πάτμος, όπου πολλά χρόνια μετά την εποχή των Ελλήνων ο χριστιανός Ιωάννης γράφει στην αρχή του βιβλίου του και πάλι: “Εν αρχή ην ο λόγος”. Και ο λόγος για αυτόν είναι και πάλι μια σχέση, η ίδια σχέση που είχαν βρει οι Έλληνες, αφού λέει: “Ο Θεός είναι για τον Υιό του ό,τι ο Υιός για τον άνθρωπο”. Αναφέρει λοιπόν πάλι την σχέση και την ισότητα δύο σχέσεων. Κι έτσι, σε ένα τόπο τόσο δα σαν το μαντήλι της τσέπης που με βαρκούλα με πανί τον γυρίζεις σε δυο μέρες – ανάμεσα στις ακτές της σημερινής Τουρκίας και κάποια νησιά διάσπαρτα κατά μήκος αυτών των ακτών – βρίσκεται εκεί όπου πριν από δύο χιλιετίες γεννήθηκε αυτό που όξυνε το πνεύμα μας. Δηλαδή ο “λόγος”, η σχέση στην ελληνική γλώσσα.

Για να κατανοήσουμε σωστά το ελληνικό πνεύμα ας φανταστούμε το εξής: Σε ένα χάρτη η Βαβυλώνα είναι το κέντρο του κόσμου, ο ποταμός που την βρέχει, ο Ευφράτης, είναι ο κύριος ποταμός του κόσμου και οι λαοί τριγύρω είναι μακρινοί και κάπως ξεχασμένοι, περιφρονημένοι. Αν συγκρίνετε αυτόν τον χάρτη με αυτόν τον ελληνικό χάρτη που μάλλον σχεδιάστηκε από τον Αναξίμανδρο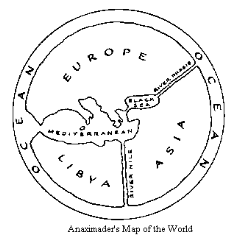

θα δείτε πως ο ελληνικός χάρτης είναι παγκόσμιος. Υπάρχουν εκεί όλοι ανεξαιρέτως οι κατοικημένοι τόποι. Η Ελλάδα έχει εξέχουσα θέση μα φαίνεται όλη η Μεσόγειος και ο τότε κόσμος παρουσιάζεται κυκλικός και περιβάλλεται ολόκληρος από τον ποταμό Ωκεανό. Από τη μια, ο “ιδιαίτερος” χάρτης ενός λαού που θεωρεί τη ζωή του κέντρο του κόσμου και από την άλλη ένας χάρτης ήδη παγκόσμιος, πανανθρώπινος.

“Τον άντρα τον πολύτροπο πες μου θεά, που χρόνια παράδερνε, σαν πάτησε της Τροίας το άγιο κάστρο κι ανθρώπων γνώρισε πολλών τον τόπο και την γνώση κι έπαθε μύριες συμφορές στα πέλαγα, ζητώντας πώς στην πατρίδα του άβλαβος να πάει με τους συντρόφους”.

Βορέας, Καικίας, Απηλιώτης, Εύρος, Νότος, Λιψ, Ζέφυρος, Σκίρων. Ιδού οι άνεμοι που φυσούν πάνω στη γη. Αντιπροσωπεύουν τα οκτώ σημεία του ορίζοντα. Αυτά τα ξέρει ο Οδυσσέας όταν ξεκινάει το ταξίδι του από την Ιθάκη σε όλη τη Μεσόγειο. Ο Οδυσσέας είναι μάλλον ένας μυθικός εξερευνητής. Ίσως πάλι να αντιστοιχεί σε κάποιο ιστορικό πρόσωπο. Αλλά το ταξίδι του είναι μία συλλογή πολλών ταξιδιών μαζί.

Όμως γνωρίζουμε και ιστορικούς εξερευνητές όπως λόγου χάρη τον Πυθέα τον Μασσαλιώτη. Ο Πυθέας που έζησε σίγουρα τον 4ο π.Χ. αιώνα υπερβαίνει την παιδεία και την παιδαγωγία δηλαδή το ταξίδι των παιδιών αλλά και το ταξίδι του Οδυσσέα. Φεύγει από την Μασσαλία, πλέει προς το νότο, περνά τις Ηράκλειες στήλες – τα σημερινά στενά του Γιβραλτάρ – ανεβαίνει κατά μήκος των ακτών της Ισπανίας, εξερευνά τα νησιά του Πονάν (Ατλαντικού) στη Δυτική Γαλλία. Προχωρά προς τη Μάγχη και περιπλέει την Αγγλία. Αρκετοί ιστορικοί λένε πως φτάνει μέχρι και την Ισλανδία, σίγουρα όμως εξερευνά την Σκανδιναβία, δηλαδή τις τωρινές Νορβηγία, Σουηδία και τις φιλανδικές ακτές. Αποκτά λοιπόν τεράστια εμπειρία για στεριές και θάλασσες εκτός του κατοικημένου κόσμου, δηλαδή της Μεσογείου. Και είμαστε σχεδόν βέβαιοι ότι το έκανε για πολλούς λόγους. Πρώτα γιατί στη Φυσική Ιστορία του ο Πλίνιος ο Πρεσβύτερος αναφέρει πολύ λεπτομερώς ένα έργο που ίσως είχε γράψει για το οποίο δεν ξανακούσαμε ποτέ, το “Περί του Ωκεανού” και όπου εκτιμά την παλιρροιακή δύναμη στις ακτές της Βρεττάνης μέσω των ρυθμών της, και προφανώς είχε μία πολύ καλή θεωρία για να εξηγεί τους ρυθμούς της παλίρροιας με τη σελήνη και είναι σχεδόν βέβαιος πώς η επίδρασή της στις παλίρροιες ήταν γνωστή από τον 4ο αιώνα π.Χ. χάρη στον Πυθέα.

“Σε αυτόν τον ήρεμο κόλπο επιβεβαίωσα τη σχέση της σελήνης με την παλλίροια. Βλέπω την “Άρτεμι”, το πλοίο μας, σε όλη της την αίγλη, και η θάλασσα προχώρησε, μα κι υποχώρησε πιο πολύ από χθες. Η διαφορά ύψους δείχνει να είναι ογδόντα πήχεις – κατά τη γνώμη μου τεράστια!”

Επίσης έχουμε μια δική του μαρτυρία για την μικρότερη διάρκεια της μέρας ανάλογα με την εποχή. Και ο λόγος που πιστεύουμε πως έφτασε τόσο βόρεια είναι ένα κείμενό του, όπου ο Πυθέας λέει πως είδε τον ήλιο να ανατέλλει αμέσως μετά την δύση. Άρα, πρέπει να έφτασε σε μεγάλο γεωγραφικό βάθος το καλοκαίρι. Κι εκείνη την εποχή υπάρχει μόνο η δική του μαρτυρία σχετικά με την διαφορά στη διάρκεια της ημέρας.

“Ο ήλιος φάνηκε επιτέλους  ανάμεσα από τα γκρίζα σύννεφα. Κατάφερα να υπολογίσω τους αριθμούς που προσδιορίζουν τη σχέση ανάμεσα στη σκιά και το ύψος του γνώμονά μου. Πλησιάζουμε στο ηλιοστάσιο και η μέρα εδώ είναι πιο μεγάλη από ό,τι στη χώρα των Βόρειων Βρετανών. Διαρκεί πάνω από 18 γυρίσματα της κλεψύδρας. Όταν προσπαθούσα να δώσω στους ιθαγενείς να καταλάβουν πώς ήθελα να πάω στην Θούλη, αυτοί οι βάρβαροι μάς έδειξαν που δύει ο ήλιος, τον τόπο όπου ο ήλιος έχει το θρόνο και το κρεβάτι του γιατί εκεί γέρνει και από εκεί υψώνεται.”

Επίσης αποδεικνύεται από άλλους ιστορικούς πως ο Πυθέας ανκάλυψε την έννοια του γεωγραφικού πλάτους. Και πώς επινόησε το γεωγραφικό πλάτος; Όλοι νομίζουμε πως το ηλιακό ρολόι δείχνει των ώρα. Για τους Έλληνες, το ηλιακό ρολόι δεν έδειχνε την ώρα. Ήταν ένα αστρονομικό παρατηρητήριο. Κι αυτό έδειχνε το μήκος της σκιάς την πιο σύντομη ημέρα και το μήκος της σκιάς την πιο μεγάλη ημέρα, δηλαδή το χειμερινό και το θερινό ηλιοστάσιο. Έδειχνε επίσης το μήκος της σκιάς την ημέρα της ισημερίας. Η γωνία που σχηματίζει η ακμή του γνώμονος ή του ρολογιού με τη θέση της σκιάς την ημέρα της ισημερίας είναι ακριβώς η γωνία του γεωργαφικού πλάτους. Αυτήν την ανακάλυψη την έκανε πρώτος ο Πυθέας. Είδε πως αυτή η γωνία έδειχνε πόσο ψηλά ήταν αυτό το μέρος.

“Από τη σχέση του μήκους του γνώμονος και της σκιάς του, βεβαιώνω πως αυτή τη στιγμή, απέχουμε 9.000 στάδια από τη Μασσαλία, πάνω από τη διάμεσο του κόσμου. Η ημέρα τώρα διαρκεί σχεδόν 18 γυρίσματα της κλεψύδρας αλλά οι βάρβαροι μού εξήγησαν ότι όλο το χειμώνα ο ήλιος ανεβαίνει μόνο 9 πήχεις πάνω από τον ορίζοντα πράγμα που συμπίπτει με το ύψος του ήλιου στη Μασσαλία.“

Στον επινοητή του γεωγραφικού πλάτους μπορούν να απονεμηθούν τρεις τίτλοι ταυτόχρονα:  Του αστρονόμου, αφού το ηλιακό ρολόι είναι αστρονομικό όργανο. Του γεωγράφου, αφού ορίζει το γεωγραφικό πλάτος ενός τόπου. Και του γεωμέτρη, αφού όλα αυτά τα ανακαλύπτει χάρη στο θεώρημα ισότητας των εναλλάξ γωνιών. Γιατί, για να βρούμε τη γωνία του γεωγραφικού πλάτους χρειάζεται και μία ορισμένη επεξεργασία του σχήματος που δείχνει ο γνώμονας. Κι εκεί ακριβώς το παράδειγμά του είναι ενδιαφέρον ως προς το συχετισμό θρύλου και ιστορίας. Δηλαδή τη σχέση που μπορεί να υπάρχει ανάμεσα στην εξερεύνηση της γης, τη χαρτογράφηση και μέτρησή της και τα γεωγραφικά σχήματα, δηλαδή τα σημεία, τις γωνίες, τις ευθείες και τις μονάδες μέτρησης.

“Η “Άρτεμις” πλέει μέσα σε κάτι άγνωστο που μόνο πνεύμονα της θάλασσας μπορώ να το ονομάσω. Δεν είναι ούτε σκληρός πάγος, ούτε αέρας, ούτε νερό.”

Λέγεται πως  ο Θαλής ταξίδεψε στην Αίγυπτο κι έβλεπε τον ήλιο να ανατέλλει και να δύει πίσω από τις τρεις μεγάλες πυραμίδες. Και μετρώντας τη σκιά των πυραμίδων στον ήλιο συχέτισε αυτήν την σκιά με τη σκιά που έριχνε το δικό του σώμα την ίδια στιγμή. Ιδού λοιπόν η πυραμίδα όρθια, η μακριά σκιά που απλώνεται κατάμαυρη πίσω από την πυραμίδα κι ο άνθρωπος όρθιος με την σκιά του στην άμμο: δύο τρίγωνα. Και παρατηρεί πως υφίσταται η ίδια σχέση ανάμεσα στην πυραμίδα και την προβολή της σκιάς της και ανάμεσα στο σώμα του και την προβολή της σκιάς του. Κι έτσι επινοεί το περίφημο θεώρημα των όμοιων τριγώνων.

Αυτό το θεώρημα είναι το θέωρημα της κλίμακας. Δηλαδή, μπορούμε να αναπαραστήσουμε κάτι αν διατηρήσει το σχήμα αλλά όχι και το μέγεθός του; Ίδιο σχήμα, διαφορετικό μέγεθος – δηλαδή ακριβώς το πρόβλημα της κλίμακας. Βλέπουμε λοιπόν πως μπορούμε και πάλι όπως τον καιρό του Πυθέα του Μασσαλιώτη να συσχετίσουμε την γεωγραφία, το πρόβλημα του χάρτη, της αναπαράστασης, της κλίμακας, με την γεωμετρία, την επινόηση του θεωρληματος των όμοιων τριγώνων του πρώτου θεωρήματος στην ιστορία – συνεπώς με την επινόηση της ίδιας της γεωμετρίας.

Από την Αίγυπτο ως τα μέρη των αιώνιων πάγων, από τον ουρανό του Νότου ως αυτόν του Βορρά, από το Νότιο ως το Βόρειο ημισφαίριο, το ταξίδι του Πυθέα είχε επιτρέψει τη χαρτογράφηση της γης, μα κατά κάποιο τρόπο και του ουρανού. Ο ουρανός της Ελλάδος δεν ήταν ο ίδιος με της Ισλανδίας που είχε ανακαλύψει ο Πυθέας ούτε της Αιγύπτου, όπου είχαν πάει ο Θαλής και ο Ερατοσθένης. Χάρη στο ταξίδι είχαν μεγαλώσει γη και ουρανός μαζί. Ακόμα και ο Οδυσσέας θα έβλεπε κοντά στην σημερινή Τυνησία αστερισμούς που δεν μπορούσε να δει στον ουρανό της Ιθάκης.

Για να παρατηρήσεις τον ουρανό χρειάζεσαι ένα αστεροσκοπείο. Οι Έλληνες δεν είχαν. Δεν το είχαν ανάγκη αφού είχαν έναν άξονα στο έδαφος, ηλιακό ρολόι και γνώμονα. Ιδού μια έκλειψη σελήνης. Βλέπουμε τη σκιά της γης που έρχεται αργά να καλύψει τη σελήνη. Οι Έλληνες γνώριζαν το μέγεθος της γης. Το είχε μετρήσει ο Ερατοσθένης. Η σκιά της γης είναι 3-4 φορές μεγαλύτερη από της σελήνης. Οι Έλληνες γνώριζαν το μέγεθος της σελήνης. Ο Αρίσταρχος ο Σάμιος υπολόγιζε τη σχετική απόσταση ήλιου και σελήνης από τη γη μετρώντας πάνω σε ένα όσο το δυνατόν πιο ακριβές τρίγωνο κατά το ορθογώνιο τρίγωνο που σχηματίζουν τα 3 σώματα όταν η σελήνη βρίσκεται σε τέταρτο και για να οριστεί τρίγωνο αρκεί να μετρηθεί η γωνία της με τη γη. Όπως ο Θαλής, έτσι κι ο Αρίσταρχος φτιάχνει πρότυπα υπό κλίμακα για τέτοιες μελέτες περιπτώσεων της αστρονομίας. Το απρόσιτο μετράται με την αναπαραγωγή ή τη μίμηση μέσα στα όρια του προσιτού. Αυτό κάνει ο Θαλής, ο Αρίσταρχος καικάθε πρωτοπόρος.

Κάποια άστρα στον ουρανό κινούνται. Μπορούμε να παρακολουθήσουμε την πορεία τους ειδικά ενός από αυτά που μοιάζει να πηγαινοέρχεται. Είναι ο πλανήτης Άρης. Πώς εξηγείται αυτό το παράδοξο; Υπάρχουν δύο σφαίρες, η μία μέσα στην άλλη. Η μία περιέχει τα σταθερά ουράνια σώματα η άλλη τα κινούμενα, τους πλανήτες. Αυτή η κίνηση εξηγεί το σύμπαν. Αυτή η συνδυασμένη κίνηση δημιουργεί μια καμπύλη. Ο Εύδοξος την αποκαλούσε “Ιπποπέδη”. Σήμερα ξέρουμε πως τα άστρα δεν συγκρατούνται από σφαίρες. Τα συγκρατεί μια δύναμη, η συμπαντική βαρύτητα. Αλλά η εξήγηση του Εύδοξου έχει αξία αφού πρότεινε ένα πρότυπο.

Από τις απαρχές της, η ελληνική αστρονομία ξεχωρίζει σε σχέση με τις παλαιότερες ή σύγχρονες της αστρονομίες για την εκπληκτική ακρίβεια του γεωμετρικού προτύπου της. Οι Έλληνες είχαν ένα πράγμα κατά νου, και το έλεγαν συχνά: Τι είναι αυτό που βλέπω και πώς θα το εξηγήσω; Η λέξη “φαινόμενο” είναι ελληνική: Αυτό που φαίνεται. Πίσω από αυτό που φαίνεται υπάρχει μια αιτία. Και αυτή η αιτία εξηγείται πάντα γεωμετρικά. Οι Έλληνες, π.χ. από την αρχή της ιστορίας τους ως τον Πτολεμαίο, στα τέλη της ελληνιστικής περιόδου δίσταζαν πραγματικά στη σκέψη αν κέντρο του κόσμου είναι ο ήλιος ή η γη. Συνεπώς, υπάρχουν δύο πιθανές εκδοχές: ο γεωκεντρισμός με τη γη στο κέντρο του κόσμου και ο ηλιοκεντρισμός, με τον ήλιο στο κέντρο του κόσμου. Κι αν υποθέσουμε ότι το πρώτο είναι το σωστό υπάρχει ένα γεωμετρικό πρότυπο που το εξηγεί. Πώς περιστρέφονται οι πλανήτες γύρω από τον ήλιο; Πώς περιστρέφεται η γη γύρω από τον ήλιο; Και αν αληθεύει η υπόθεση του γεωκεντρισμού πώς περιστρέφονται οι πλανήτες γύρω από τη γη; Πώς περιστρέφονται τα άστρα γύρω από τη γη; Και ένα νέο γεωμετρικό πρότυπο τα εξηγεί όλα αυτά. Σε αυτήν την περίπτωση, έλεγαν, υπάρχει ισοτιμία υποθέσεων. Από τη στιγμή που μπορώ να εξηγήσω με λογικό τρόπο και την κίνηση του κόσμου σύμφωνα με την πρώτη υπόθεση και την κίνηση του κόσμου σύμφωνα με την δεύτερη τα δύο πρότυπα είναι ισότιμα.

Δεν υπάρχουν στις θεωρίες ιδέες τόσο σαφείς, τόσο ακριβείς και τόσο ελαστικές. Οι Έλληνες ενέταξαν το πρότυπο της γεωμετρίας στην αστρονομία. Από τότε η επιστήμη επέλεξε αυτό το δρόμο μια για πάντα.

Είναι ένας δρόμος που δεν μας έλειψε ποτέ.